جایزه چشمگیر ۳۰ میلیارد تومانی برای کسی که حتی یکی از این مسائل را حل کند!

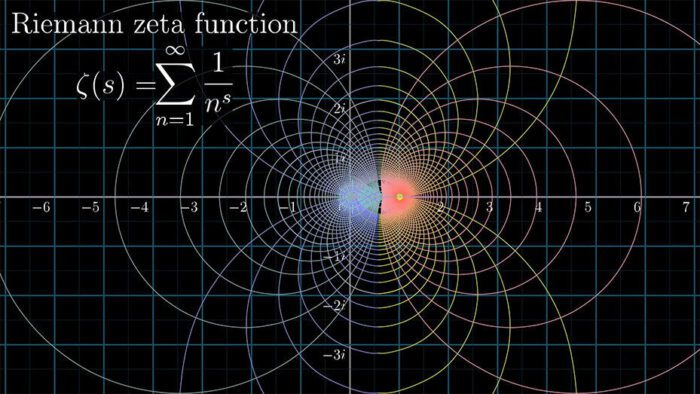
مهم‌ترین مسئله‌ی حل نشده در ریاضیات محض به فرضیه ریمان (Riemann Hypothesis) مشهور است. این مسئله را برنهارت ریمان، ریاضیدان آلمانی قرن نوزدهم مطرح کرده است که آثارش در زمینه آنالیز و هندسه دیفرانسیل، پایه ریاضی نظریه‌ی نسبیت عام شد.

فرضیه ریمان از سال ۱۸۵۹ تاکنون حل نشده باقی مانده و به‌قدری دشوار است که دیوید هیلبرت، از تأثیرگذارترین ریاضیدانان در پیدایش و گسترش مکانیک کوانتومی و نظریه نسبیت، درباره‌ی آن گفت:‌

اگر قرار بود بعد از هزار سال از خواب بیدار شوم، اولین سوالی که می‌پرسیدم این بود: آیا فرضیه ریمان اثبات شده است؟

جالب است بدانید هیلبرت در سال ۱۹۰۰، بیست و سه سؤال ریاضی که تا آن زمان حل نشده بودند را مطرح کرده بود که فرضیه ریمان یکی از آن‌ها بود. برخی از این سؤال‌ها که به مسائل هیلبرت شهرت دارند، حل شده‌اند و تأثیر بسزایی بر ریاضیات قرن بیستم گذاشتند.

فرضیه ریمان درواقع از شما می‌خواهد اثبات کنید تابع زتا ریمان در چه شرایطی برابر با صفر است. ریمان می‌گوید تابع زتا تنها زمانی به صفر می‌رسد که با اعداد صحیح زوج منفی و اعداد مختلط با قسمت واقعی ۱/۲ سروکار داشته باشیم. مشکل اینجا است که اگرچه بیش از ۲۵۰ میلیون صفر این فرضیه را اثبات کرده‌اند، هنوز ثابت نشده که این موضوع برای تمام صفرها صدق می‌کند.

فرضیه ریمان از این جهت بسیار مهم است که اعداد اول (که فقط بر یک و خودشان تقسیم‌پذیرند) اساسی‌ترین و اسرارآمیزترین مفهوم در ریاضیات هستند. وقتی اعداد اول را به صورت مجموعه خطی پشت سر هم می‌نویسیم، هیچ الگویی در نحوه توزیع آن‌ها ظاهر نمی‌شود و به‌همین خاطر نمی‌توانیم تمام اعداد اول را پیش‌بینی کنیم. اما وقتی این اعداد را به کمک تابع زتا ریمان روی نمودار می‌آوریم، الگوی جالبی از صفرهای ریمان روی آن ظاهر می‌شود که اگر بتوانیم آن را برای تمام اعداد ثابت می‌کنیم، آن‌وقت می‌توانیم بگوییم الگوی پنهان توزیع اعداد اول را سرانجام کشف کرده‌ایم. بدین‌ترتیب می‌توانیم با دقت بسیار بالا تعداد اعداد اول در هر بازه معینی را تعیین کنیم.

شاید بپرسید داشتن تابعی برای تعریف اعداد اول اصلاً چه اهمیتی دارد؟ بسیاری از ریاضیدانان اعداد اول را به‌عنوان اتم‌های تشکیل‌دهنده‌ی تمام اعداد دیگر می‌بینند، زیرا می‌توانید با استفاده از اعداد اول به هر عددی برسید. در فرضیه ریمان، دامنه‌ای که روی خط عددی از مقادیری ایجاد می‌شود که تابع زتا را صفر می‌کند، همانند فواصل بین سطوح انرژی در سیستم‌های کوانتومی است و این یعنی نوعی رابطه بین اجزای سازنده اعداد با اعداد اول و اجزای سازنده ماده با اتم وجود دارد و حل این فرضیه ما را به درک جدیدی از ماده خواهد رساند.

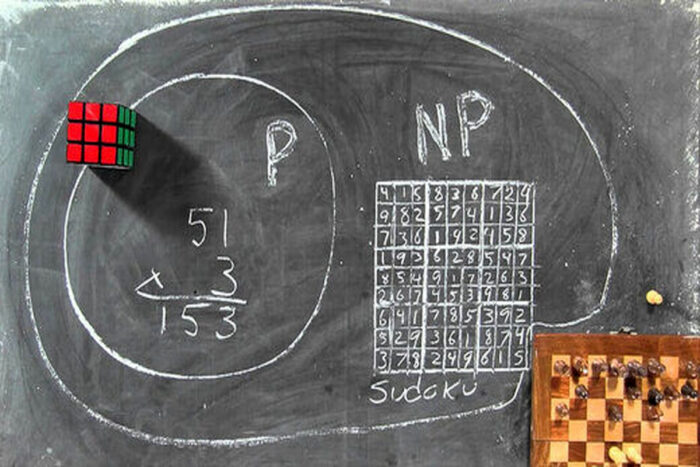
مسئله P در مقابل NP

P درمقابل NP مسئله حل نشده مهمی در علوم کامپیوتر است و می‌پرسد آیا هر مسئله‌ای که صحت جواب‌های آن را بتوان به‌سرعت ارزیابی کرد (NP)، به‌سرعت هم قابل حل‌شدن است (P)؟ این مسئله را استیون کوک، دانشمند کامپیوتر در سال ۱۹۷۱ مطرح کرد.

بیایید برای فهم بهتر این مسئله یک مثال بزنیم. اگر به شما عددی را بدهند و بگویند این عدد از حاصل‌ضرب کدام دو عدد اول بدست آمده است، آیا می‌توانید به پاسخ درستی برسید؟ اگر این عدد کوچک باشد، جواب ساده است. مثلاً ۱۵ از ضرب دو عدد ۵ و ۳ حاصل می‌شود. اما اگر عدد موردنظر ما ۲۰۰ رقم داشته باشد، سال‌ها زمان لازم است تا دو مضرب آن پیدا شود.

در حوزه علوم کامپیوتر، مسئله‌ای که جوابش به‌سرعت تعیین می‌شود، P و مسئله‌ای که صرفاً صحت جواب‌های آن به‌سرعت تأیید می‌شود، NP نام دارد. درواقع، اینکه مسائل بتوانند به‌سرعت حل شوند، یا به زبان علوم کامپیوتر، زمان اجرای الگوریتم آن‌ها «چندجمله‌ای» (Polynomial Time) باشد، از اهمیت بسیاری برخوردار است؛ چراکه اگر حل مسئله‌ای بخواهد صدها یا هزاران سال طول بکشد، حل آن عملا ناممکن است.

مسئله استیون کوک دقیقاً این را می‌پرسد:آیا می‌توانیم در ازای هر الگوریتم NP که زمان اجرای آن چند جمله‌ای است، الگوریتمی با زمان اجرای چند جمله‌ای برای P داشته باشیم؟

روزی که کسی بتواند سرانجام ثابت کند P=NP، بسیاری از ریاضیدانان از کار بی‌کار می‌شوند. چراکه P=NP به این معنی است که اثبات یک نظریه ریاضی با ارزیابی صحت جواب‌های آن یکی است. حتی بدتر از آن، تمام سیستم‌های بانکی نیز از کار می‌افتند؛ چراکه رمزگشایی از کلمات‌عبور که با مضرب بسیار بزرگی از اعداد اول رمزنگاری می‌شوند، در کسری از ثانیه ممکن می‌شود. برای آشنایی بیشتر با این موضوع پیشنهاد می‌کنم مقاله الگوریتم شور به زبان ساده؛ رمزگشایی داده در کامپیوتر کوانتومی را مطالعه کنید.

حدس هاج

حدس هاج (Hodge Conjecture) یکی از مسائل مهم حل نشده در هندسه جبری و هندسه مختلط است که چگونگی تشکیل ساختارهای پیچیده‌ی ریاضی از اجزای ساده را بررسی می‌کند و درواقع می‌کوشد این دو مفهوم مختلف ریاضی را به هم پیوند دهد.

در قرن بیستم، ریاضیدانان روش مهمی برای مشاهده و بررسی اجسام پیچیده کشف کردند؛‌ به‌این صورت که اجسامی را که به‌طور فزاینده‌ای بزرگ‌تر می‌شدند، کنار هم قرار می‌دهند تا به نزدیک‌ترین شکل به جسم اصلی برسند. این تکنیک به‌قدری مفید بود که در بسیاری از حوزه‌های دیگر نیز به کار گرفته شد و درنهایت، اجسام پیچیده‌ای که ریاضیدانان به‌ این روش دسته‌بندی کردند، در اختراعات شگفت‌انگیزی به کار رفتند.

متأسفانه، ازطریق این تعمیم‌ها، خاستگاه هندسی این فرایند از بین رفت و تلاش بر این بود که این اجزا بدون فرمول و پشتوانه هندسی به هم پیوند داده شوند. حالا حدس هاج می‌پرسد آیا برای این مفهوم، رابط هندسی وجود دارد؟

نظریه یانگ-میلز

در طول شش دهه‌ی گذشته، تئوری یانگ-میلز به سنگ بنای فیزیک نظری تبدیل شده است؛ چراکه به نظر می‌رسد تنها نظریه نسبیت کوانتوم چندجسمی کاملاً سازگار با چهار بعد فضازمان باشد و به‌همین خاطر، پایه مدل استاندارد فیزیک ذرات است که ثابت شده نظریه درستی برای انرژی‌هایی است که می‌توانیم اندازه‌گیری کنیم.

نظریه یانگ-میلز درواقع تعمیم نظریه یکپارچه الکترومغناطیس یا همان «معادلات ماکسول» است که توسط جیمز کلرک ماکسول، فیزیکدان اسکاتلندی مطرح شد و برای توصیف نیروی ضعیف و نیروی قوی ذرات زیراتمی بر حسب ساختار هندسی یا میدان کوانتومی به کار می‌رود.

این نظریه در سال ۱۹۵۴ توسط دو فیزیکدان به نام‌های چن نینگ یانگ و رابرت ال. میلز ارائه شد و بر خاصیت مکانیک کوانتومی موسوم به «شکاف جرم» (Mass Gap) تکیه دارد که درواقع تفاوت انرژی بین پایین‌ترین سطح (خلا) با کمترین سطح بعدی و معادل جرم سبک‌ترین ذره است. دانشمندان معتقدند شکاف جرمی عاملی است که باعث شده نیروی قوی تنها در فواصل بسیار کوچک، یعنی درون هسته‌های اتمی،‌ وجود داشته باشد.

نظریه یانگ‌میلز یکپارچگی نیروی الکترومغناطیسی و نیروی ضعیف را توصیف می‌کند؛ نیروی اول باعث می‌شود الکترون‌ها به دور پروتون بچرخند و نیروی دوم باعث می‌شود یک نوترون به یک الکترون و یک پروتون تجزیه شود. تفاوت این دو نیرو مانند تفاوت بین قمری است که در حین چرخش به دور سیاره دور خود می‌چرخد و قمری که در حین چرخش به دور سیاره، به‌دور خود نمی‌چرخد. نیرویی که قمر را در مدار سیاره نگه می‌دارد، صرف‌نظر از اینکه به دور خود می‌چرخد یا خیر، یکسان است. منظور از یکپارچگی همین است؛ اینکه نشان دهیم پشت این دو چیز متفاوت، نیروی یکسانی وجود دارد.

معادلات ناویه–استوکس

معادلات ناویه-استوکس (Navier Stokes Equations) یکی دیگر از مسائل جایزه هزاره است که به مجموعه‌ای از معادلات دیفرانسیل مربوط می‌شود که حرکت سیالات تراکم‌پذیر را توصیف می‌کند. به‌طور خلاصه، معادلات ناویه-استوکس رفتار سیالات را توصیف می‌کند.

این معادلات اگرچه ساده به نظر می‌ٰسند، در حالت سه‌بعدی به‌سرعت پیچیده می‌شوند. چارلز ففرمن، استاد دانشگاه پرینستون می‌گوید: «می‌توان حل معادلات ناویر-استوکس را نسبتاً به‌سادگی و با اعتماد به نفس بالا شروع کنید؛ اما راه‌حل‌ها ممکن است به‌طور باورنکردنی‌ای غیرقابل پیش‌بینی باشند».

گفته می‌شود اگر ریاضیدانان بتوانند پدیده ناویه-استوکس را از این حالت غیرقابل پیش‌بینی بیرون آورند، تغییرات شگرفی در زمینه دینامیک سیالات حاصل خواهد شد. به گفته‌ی ففرمن، اگر این معادلات به اثبات برسد، «دستاوردی فوق‌العاده در بالاترین حد خواهد بود.»

حدس برش و سوینرتون-دایر

اوایل دهه ۱۹۶۰ در انگلستان، ریاضیدانان بریتانیایی برایان برش و پیتر سوینرتون-دایر از کامپیوتر EDSAC که جزو اولین کامپیوترهای ساخت انگلیس بود، برای انجام تحقیقات عددی منحنی‌های بیضوی استفاده کردند. آن‌ها براساس این نتایج عددی، حدس برش و سوینرتون-دایر (Birch and Swinnerton-Dyer conjecture) را مطرح کردند که آخرین مسئله حل‌نشده یک میلیون دلاری در این فهرست است.